
The Naive Bayes classifiers are a relatively simplistic group of statistical models for assigning class labels to a given input. The predictions are based on comparing how likely the input would be observed in each class.
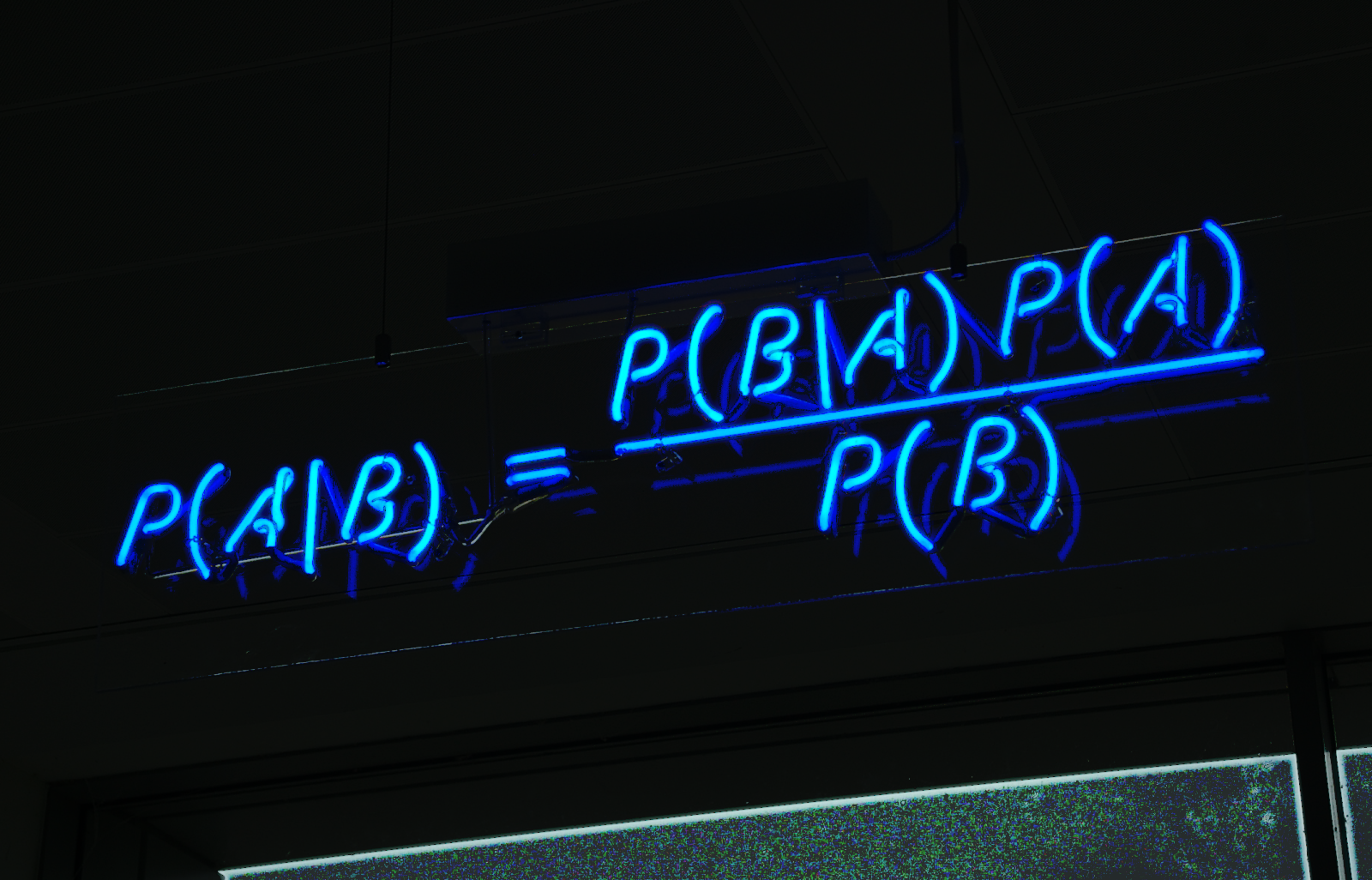
This is Bayes Theorem and it states: the probability of A given B is equal to the quantity of the probability of B given A
times the probability of A divided by the probability of B.
A more intuitive way to understand this conditional probability is to use Bayesian terminology:
The calculated probability is equal to the probability of the class times the probability of each input occurring in that class.
Dividing by the evidence is included in the probability of each input occuring in that class.
The standard example given here is classifying email as spam or non-spam. The Naive Bayes model is supervised learning,
which means that it is trained on labeled data. Emails labeled as spam or non-spam are inputted into the Naive Bayes classifier, and the model calculates how much each word
is associated with spam or non-spam based on frequency in each class.
There are 3 flavors of Naive Bayes classifiers: Bernoulli, Multinomial, and Gaussian. These correspond to the distribution of the features being analyzed.
- Bernoulli distribution is binary, did X occur or not?
- Multinomial distribution is discrete, often the frequency or count of X.
- Gaussian distribution is also known as the normal distribution for continuous variable, could be a measurement like 88.2mL
I will use the multinomial distribution because I am interested in the number of times a word appears in a category instead of just whether it appears or not.
What’s the Naive part of Naive Bayes?
The naivete in this regard comes from assuming that all probabilities are independent. In the email example this means that the probability of finding the word “Timeshare”
isn’t affected by seeing the words “Limited Offer”. This is often and easily violated, especially in the context of natural language. However, despite the relatively simplistic model,
it produces good results.
I will be coding a multinomial Naive Bayes classifier from scratch in Python. The main goals are to be able to fit it on labeled documents, and to use it to predict labels on new inputs.
I’ll need to have several data preprocessing steps to handle text input into this model. The first I will use to tokenize the document:
def tokenize(self, document):
"""
Take in a document and return a list of words
"""
doc = document.lower()
# remove non-alpha characters
stop_chars = '''0123456789!()-[]{};:'"\,<>./?@#$%^&*_~'''
tokens = ""
# iterate through and make each token
for char in doc:
if char not in stop_chars:
tokens += char
return tokens.split() # now a list of tokens
Tokenizing entails processing a document into a list of words, removing unwanted characters. Next I had to create a dictionary with the word counts per class.
A key piece to writing this class was making sure you had access to prior probabilities for future usage in the overall theorem.
def prior_prob(self, counts):
# Iterate through counts dict and add up each word count by category
cat0_word_count = cat1_word_count = 0
for word, (cat0_count, cat1_count) in counts.items():
cat0_word_count += cat0_count
cat1_word_count += cat1_count
# save attributes to the class
self.cat0_count = cat0_word_count
self.cat1_count = cat1_word_count
self.total_count = self.cat0_count + self.cat1_count
# Get the prior prob by dividing words in each cat by total words
cat_0_prior = cat0_word_count / self.total_count
cat_1_prior = cat1_word_count / self.total_count
return cat_0_prior, cat_1_prior
cat0 and cat1 refer to the two categories, represented in the data as the labels ‘0’ and ‘1’. In order to get the probablities for each word you simply take the number of times the word appeared in a class and divide by the total number of words in that class. But what if that word doesn’t appear in another class? That would yield a probability of 0 and if that were to be multiplied by any other calculation, the whole expression would be rendered meaningless. The solution is to use something called Laplace Smoothing. The idea behind smoothing is that you can add a small base amount to every word probability so that computations can still be run on the whole input. I use the variable k to denote the smoothing coefficient.
It’s time to draw open the curtains for the main show! The fit method puts everything to use, preprocessing the input and calculate all the probabilities on the training data.
The predict method was the toughest part of the implementation.
def fit(self, X, y):
# Take all these functions and establish probabilities of input
counts = self.count_words(X, y)
self.cat_0_prior, self.cat_1_prior = self.prior_prob(counts)
self.word_probs = self.word_probabilities(counts)
def predict(self, test_corpus):
# Split the text into tokens,
# For each category: calculate the probability of each word in that cat
# find the product of all of them and the prior prob of that cat
y_pred = []
for document in test_corpus:
# Every document gets their own prediction probability
log_prob_cat0 = log_prob_cat1 = 0.0
tokens = self.tokenize(document)
# Iterate through the training vocabulary and add any log probs that match
# if no match don't do anything. We just need a score for each category/doc
for word, prob_cat0, prob_cat1 in self.word_probs:
if word in tokens:
# Because of 'overflow' best to add the log probs together and exp
log_prob_cat0 += np.log(prob_cat0)
log_prob_cat1 += np.log(prob_cat1)
# get each of the category predictions including the prior
cat_0_pred = self.cat_0_prior * np.exp(log_prob_cat0)
cat_1_pred = self.cat_1_prior * np.exp(log_prob_cat1)
if cat_0_pred >= cat_1_pred:
y_pred.append(0)
else:
y_pred.append(1)
return y_pred
self.word_probs consists of a list of triplets: word, p(word | cat0), and p(word | cat1). I iterate through every word, check if it’s in the inputted document, if so then add the log probability of each class. The logarithmic function is necessary here to handle “underflow”, where if you multiply many fractions, the number approaches 0 and becomes difficult to keep track of. After accruing all the log(probabilities) we can convert it back to a regular probability by using Euler’s number, e raised to the log(probability). Finally, I compare the total probability that the input came from either class and return the class with the higher probability.
To test my class, I used pytest and pulled data from two different subreddits to train and test on. By predicting on documents in the respective classes I could test that the model was consistent internally.
```def test_nb_class():
# fit an instance and test it against 2 docs of each
nb = MNNaiveBayes()
nb.fit(X, y)
assert nb.predict(X[0:2] + X[-3:-1]) == [0, 0, 1, 1]
def test_sklearn(): # Need to preprocess manually cv = CountVectorizer(strip_accents=’ascii’, token_pattern=u’(?ui)\b\w[a-z]+\w\b’, lowercase=True, stop_words=’english’) X_train_cv = cv.fit_transform(X) X_test_cv = cv.transform(X_test) # sklearn naive bayes MNB = MultinomialNB() MNB.fit(X_train_cv, y) assert (MNB.predict(X_test_cv) == [0, 1, 1, 1]).all()
# our naive bayes from scratch
nb = MNNaiveBayes()
nb.fit(X, y)
assert nb.predict(X_test) == [0, 1, 1, 1] ``` I also imported scikit-learn's implementation of multinomial Naive Bayes. The inputs in this case were new entries each respective subreddit, both of scikit-learn's implementation and mine had the same prediction, misclassifying the second element.
Thanks for reading my implementation, you can find my code on my github
